Leonardo din Pisa (1170-1250), supranumit Fibonacci, s-a nascut in Pisa, Italia. A contribuit mult la dezvoltarea matematicii, dar e faimos pentru secventa de numere ce ii poarta numele:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …
Aceasta secventa e realizata prin alegerea a doua numere si repartizarea celorlalte numere prin regula ca fiecare numar trebuie sa fie suma celor doua numere precedente. Aceasta regula simpla genereaza o secventa numerica ce are multe calitati surprinzatoare. Acestea ar fi o parte din ele:
– luati oricare trei numere adiacente din secventa, ridicati la patrat numarul din mijloc, inmultiti pe primul cu al treilea numar. Diferenta dintre cele doua rezultate e intotdeauna 1.
– luati oricare patru numere adiacente din secventa. Inmultiti numerele din capete. Inmultiti pe cele din interior. Primul rezultat va fi mai mare sau mai mic cu 1 decat al doilea rezultat.
– suma a oricare zece numere adiacente e egala cu al saptelea numar din secventa inmultit de 11 ori.
Secventa Fibonacci respecta relatia recursiva P(n) = P(n-1) + P(n-2). Intr-o asemenea secventa, primele doua valori sunt alese in mod arbitrar. Ele se numesc „semintele” secventei. Atunci cand 0 si 1 sunt alese ca punct de pornire, sau 1 si 1, sau 1 si 2, secventa se numeste Fibonacci. Secventa formata din proportia numerelor adiacente converge spre valoarea constanta 1.6180339887…., numita „phi”, simbolizata prin litera greceasca Tau, t.
O trasatura deosebita a acestei secvente e faptul ca reciproca lui t este 0.6180339887… ceea ce inseamna t – 1. Intr-o alta forma, t = 1/t + 1.
Acest lucru e valabil indiferent de numerele folosite ca punct de pornire a secventei, rezultatul depinde doar de relatia recursiva folosita. Prin urmare exista mai multe secvente diferite ce converg inspre t. Ele se numesc „secvente Fibonacci generalizate”.
Proportia t = 1.6180339887… se numeste „proportia de aur”. Un dreptunghi ale carui laturi se incadreaza in aceasta proportie, se numeste „dreptunghi de aur” si era un concept aparent familiar vechilor greci. Acest dreptunghi sta la baza generarii unei curbe cunoscuta ca „spirala de aur”, o spirala logaritmica ce are coresponente in natura.
Acesta fiind principalul motiv din spatele interesului mistic-popular fata de acest subiect matematic.
Proportia de aur
Succesul enorm al cartii „Codul lui Da Vinci” a facut cunoscuta notiunea de proportie de aur unei noi audiente. Grecii antici credeau ca exista un dreptunghi pe care ochiul uman il considera foarte atragator, si ca proportiile sale sunt date de radacina pozitiva a ecuatiei cuadratice:
x² – x – 1 = 0
Ne confruntam cu aceasta ecuatie atunci cand incercam sa determinam felul in care trebuie sa impartim un segment de dreapta in asa fel incat proportia intregii linii fata de partea sa cea mai lunga sa fie egala cu proportia partii sale cele mai lungi fata de cea mai scurta. Aceasta proportie e exprimata prin „numarul de aur” (t) = 1,61803398874…, cu un numar infinit de zecimale. Inversul lui t, adica 1/t, are exact aceleasi zecimale: 0,61803398874…
Odata gasit acest numar, povestea continua. Grecii antici aparent foloseau magia numerelor in arhitectura, un bun exemplu e Panteonul din Atena. Inspirati de greci, viitoarele generatii de arhitecti si-au proiectat cladirile bazandu-se pe aceasta proportie minunata. Nici pictorii nu au ignorat-o. Se spune ca Leonardo Da Vinci folosea proportia de aur pentru a pastra proportiile figurilor umane din picturile sale – in acest fel proportia de aur a ajuns in paginile nuvelei lui Dan Brown.
Povestea e interesanta, dar… din nefericire, in afara de faptul ca Euclid a rezolvat problema divizarii liniei in cartea sa „Elementele”, nu exista alte dovezi care sa sustina afirmatiile facute in privinta proportiei de aur, dar exista motive bune sa credem ca toate afirmatiile sunt false, asa cum matematicianul George Markowsky, de la Universitatea din Maine, a indicat in articolul sau „Notiuni gresite despre proportia de aur” publicat in College Mathematics Journal in ianuarie 1992.
Dar din cauza ca povestea, care uneste matematica pura cu estetica, arhitectura si pictura, e mult mai interesanta asa, argumentele concrete nu prea au putere asupra ei.
Separarea realitatii de fictiune
Dupa cum am mentionat mai devreme, Euclid ne-a aratat cum se calculeaza aceasta proportie, dar el era interesat mai degraba de matematica decat de estetica vizuala sau de arhitectura, din moment ce numele dat de el proportiei e „raport extrem si mediu”. Termenul de „Proportie Divina”, folosit uneori in locul celui de „Proportie de Aur”, a aparut prima oara in opera unui matematician din secolul al XV-lea, Luca Pacioli. Termenul de „Proportie de Aur” e si mai recent: a aparut in 1835 intr-o carte scrisa de matematicianul Martin Ohm (fratele sau e fizicianul ce a descoperit legea lui Ohm).
Este adevarat ca Proportia de Aur (P.A.) are legatura cu pentagrama (steaua cu cinci colturi), cu cele 5 solide platonice, cu geometria fractala, cu anumite structuri cristaline si cu modelele Penrose.
Afirmatia cea mai des intalnita e ca proportiile numerelor succesive din secventa Fibonacci tind inspre P.A. ceea ce e adevarat.
Secventa Fibonacci e generata incepand cu 0 si 1 si aplicand, in mod repetat, regula conforma careia fiecare numar nou e egal cu suma ultimelor doua numere.
Deci:
0+1 = 1, 1+1 = 2, 1+2 = 3, 2+3 = 5, etc., ceea ce produce secventa 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Secventa proportiilor succesive a numerelor din aceasta secventa, adica 1/1 = 1; 2/1 = 2; 3/2 = 1.5; 5/3 = 1.666… ; 8/5 = 1.6; 13/8 = 1.625; 21/13 = 1.615…; 34/21 = 1.619…; 55/34 = 1.6176…; 89/55 = 1.6181; …, tinde intr-adevar spre P.A.
Dar acest lucru e esential pentru a intelege de ce numerele Fibonacci se regasesc in flori si plante – si chiar asa e.
De exemplu, daca se vor numara petalele unei flori, vom avea ca rezultat un numar Fibonacci. O orhidee are 3 petale, ciubotica-cucului are 5 petale, nemtisorul are 8 petale. Toate fiind numere Fibonacci.
Daca ne uitam la floarea-soarelui, vom vedea un tipar compus din 2 tipuri de spirale, una in sensul acelor de ceas, cealalta in sens invers. Daca numaram acele spirale, vom constata, ca pentru majoritatea plantelor, media e de 21 sau 34 de spirale in sensul acelor de ceas, si 34 sau 55 de spirale in sens invers. Toate fiind numere Fibonacci. Mai putin comune sunt florile cu 55 si 89, cu 89 si 144, si chiar si cu 144 si 233 de spirale. Acest fenomen apare si la alte plante. Conurile de pin au 5 spirale in sensul acelor de ceas si 8 in sens invers, ananasul are 8 spirale in sensul acelor de ceas si 13 in sens invers.
Un alt exemplu graitor e felul in care frunzele sunt pozitionate pe tulpina copacilor si plantelor. Ele se desfasoara sub forma unei spirale incolacite in jurul tulpinei. Incepand de la prima frunza, numarati cate rasuciri complete de spirala sunt pana la frunza urmatoare. Acel numar sa fie P. Totodata numarati si frunzele intalnite (excluzand-o pe prima). Vom numi acest numar Q. Coeficientul P/Q se numeste divergenta plantei. (Divergenta este caracteristica speciei de plante). Daca calculam divergenta pentru specii de plante diferite, vom constata ca numaratorul si numitorul sunt numere Fibonacci. De regula, 1/2, 1/3, 2/5, 3/8, 5/13, si 8/21 sunt proportii divergente comune.
Desi multe dintre aceste observatii exista de mai bine de o suta de ani, de abia de curand, matematicienii si savantii, a reusit sa isi dea seama ce se intampla. E doar un exemplu de eficienta a Naturii.
De exemplu, in cazul frunzelor, fiecare frunza e pozitionata in asa fel incat sa incomodeze cat mai putin frunzele de sub ea si sa fie cat mai putin incomodata de viitoarele frunze de deasupra sa.
Acesta e motivul spiralei din jurul tulpinei. A tiparului semintelor de floarea-soarelui. Natura incearca sa „cazeze” cat mai multe seminte, iar modalitatea aleasa e pozitionarea semintelor sub forma unei spirale.
Inca din secolul al XVIII-lea, matematicienii banuiau ca un singur unghi de rotatie e calea cea mai eficienta: Proportia de Aur (masurata in numarul de rasuciri per frunza, etc.). Totusi a durat mult timp ca toate aceste elemente sa fie imbinate, ultimul element fiind adaugat prin anii 1990.
Cel mai dificil unghi pentru o crestere eficienta ar fi un numar rational de rasuciri, de exemplu 2 rasuciri sau 1/2 rasuciri sau 3/8 rasuciri, deoarece ele vor produce o rasucire completa. Matematic vorbind, o rasucire prin partea irationala a unui cerc nu va realiza o rasucire completa, dar in termeni practici va fi foarte aproape de ea.
Care este unghiul care se apropie cel mai mult de un cerc complet?
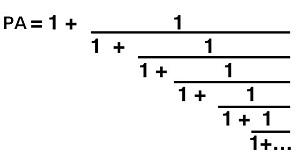
Eficienta maxima poate fi atinsa atunci cand unghiul „este cat mai departe” de a fi rational. Dar ce inseamna asta? Cea mai buna metoda, (in privinta cresterii plantei) de a constata cat de „indepartat” este un numar irational fata de unul rational, e de a vizualiza expansiunea fractiei continue. Pentru P.A. este:
Numerele rationale au o fractie continua finita. Secventa interminabila de numere din fractia continua a P.A. spune ca, masurata in termeni de fractii continue, P.A. e cat se poate de indepartata de numarele rationale. Si acesta e motivul matematic pentru care Natura foloseste P.A. ca proportie de crestere. Numerele Fibonacci apar deoarece numerele de spirale, frunze, etc. sunt numere intregi, si (datorita limitei proportiei mentionata mai devreme) numerele Fibonacci sunt cele mai bune aproximari de numere intregi pentru P.A. a cresterii.
Printre alte exemple a aparitiei P.A. in natura, se numara dezvoltarea cochiliei Nautilus si traseul urmat de soim atunci cand se coboara asupra prazii. In aceste cazuri, explicatia e ca P.A. e apropiata de spirala logaritmica, spirala ce se rasuceste la un unghi constant pe intreaga sa lungime, ceea ce o face identica in orice parte a asa.
Pe masura ce melcul se dezvolta, are nevoie, in repetate randuri, de un spatiu mai mare. Din moment ce creatura nu isi schimba forma, ci doar marimea, cea mai eficienta cale de acomodare e dezvoltarea cochiliei in forma unei spirale logaritmice.
Soimul trebuie sa aiba tot timpul prada in campul sau vizual. Desi are o vedere excelenta, pozitia ochilor e fixa si laterala. Ceea ce face soimul e sa isi incline capul, la un unghi de 40 de grade, si sa isi priveasca prada cu un singur ochi. Tinand capul inclinat la 40 de grade, soimul isi ataca prada fara sa o scape din ochi. Unghiul fix al capului sau e rezultatul spiralei cu unghiuri egale ce converge spre prada.
Acum sa trecem la miturile legate de P.A.
Problema nu e daca P.A. poate fi gasita in natura. Daca cautam suficient de mult, o sa reusim sa gasim orice numar (de marime rezonabila) oriunde. Intrebarea e daca mai exista si altceva in afara acestei numerologii aparente. Exista o explicatie stiintifica care sa ne explice de ce P.A. apare in Natura(ca in exemplele de mai sus) sau exista dovezi clare ca un anumit artist a folosit intentionat P.A. in operele sale?
Poate ca grecii antici au crezut ca P.A. e cea mai perfecta proportie pentru un dreptunghi, dar stiinta moderna nu crede asta. Numeroase teste au esuat in a demonstra existenta unui dreptunghi preferat de observatori. Preferintele pot fi influentate de multi factori. In cazul Panteonului, e suficient sa ne uitam la imaginile de care internetul e plin si sa constatam ca nu arata clar existenta P.A. (Uitati-va cu atentie la locul si felul in care e desenat acel dreptunghi, apoi intrebati-va: de ce este pus exact acolo si de ce liniile sunt atat de groase?)
Un alt mit e ca masurarea distantei dintre varful capului si podea si impartirea rezultatului la distanta dintre buric si podea, rezultatul o sa fie P.A.
Pentru inceput, nu o sa se obtina exact numarul P.A. Niciodata nu o sa se obtina, P.A. e un numar irational. Dar in cazul masurarii corpului uman, avem parte de multe variabile. E adevarat ca rezultatul va fi apropiat de 1.6. Dar nu e nimic special la acest numar. De ce sa nu zicem ca rezultatul e 1.603? Pe de alta parte, nu avem niciun motiv sa impartim corpul uman prin buric. Daca masuram diferite parti ale corpului si organizam rezultatele, vom vedea ca exista perechi de numere a caror proportie e apropiata de 1.6, de 1.5, sau de alt numar.
Apoi exista mitul ca Leonardo Da Vinci credea ca P.A. e proportia dintre inaltimea si latimea unei fete „perfecte” umane si ca a folosit P.A. in realizarea omului vitruvian. Desi nu exista dovezi impotriva acestei idei, nu exista nici dovezi in favoarea ei, asa ca singurul motiv de a crede in aceasta idee e credinta insasi. Acelasi lucru e valabil si in cazul lui Boticelli si pictura sa faimoasa „Nasterea lui Venus” sau in cazul lui Georges Seurat si pictura sa, „Parada unui circ”.
Exista si pictori ce au folosit intentionat P.A. Printre acestia se numara Paul Serusier, Juan Gris, Giro Severini si Salvador Dali. Dar acestia se pare ca au folosit P.A. doar ca tehnica experimentala, ci nu ca motiv intrinsec estetic. Cubistii au organizat, la Paris, in 1912 ,o expozitie numita „Section d’Or” dar numele nu avea nicio legatura cu arta expusa.
Exista si miturile despre piramidele si mormintele egiptene ce au fost construite cu ajutorul P.A. Nici in acest caz nu exista dovezi care sa sustina aceasta afirmatie. Tot asa cum nu exista nici dovezi care sa sustina ideea ca unele tablete de piatra indica faptul ca babilonienii cunosteau conceptul de P.A.
Revenind la arhitectura moderna…
Desi este adevarat ca faimosul arhitect francez Corbusier promova si folosea P.A. in arhitectura, ideea ca multe dintre cladirile moderne se bazeaza pe dreptunghiul de aur, printre ele fiind cladirea Secretariatului General al Natiunilor Unite, nu este fondata. In urma unui sondaj realizat printre arhitecti, a reiesit ca majoritatea lor erau familiarizati cu ideea P.A., dar nu o foloseau, desi erau convinsi ca colegii lor o folosesc.
Proportia de Aur se gaseste pana si in muzica. Printre mituri se numara si unele cantece gregoriene ce se bazeaza pe P.A., faptul ca Mozart a folosit P.A. in unele compozitii, si ca Bartok a facut la fel. Toate aceste afirmatii nu beneficiaza de nicio dovada. Si mai incert e cazul lui Debussy si daca a folosit sau nu P.A. in muzica sa. Expertii nu pot cadea de acord daca unele tipare P.A. ce sunt recunoscute, au fost intentionate sau intamplatoare.
Nici macar poezia nu este imuna la asa ceva. Dar aici avem parte de o surpriza placuta. Desi ideea ca poetul roman Vergilius si-a bazat poezia hexametrica „Eneida” pe P.A. nu e dovedita, este adevarat faptul ca unele poeme sanscrite au fost bazate pe secventa Fibonacci (prin urmare fiind legate de P.A.)
Exemplele pot continua, de la cele sacre (dimensiunile Chivotului Legii) la cele profane (prezicerea fluctuatiilor bursiere), dar toate exemplele, la o examinare mai atenta, duc lipsa de dovezi. Dar aceasta lipsa de dovezi, iar in unele cazuri existenta unor dovezi contrare, nu impiedica ca fiecare dintre aceste mituri sa aiba grupul sau de devotati, ce nu vor lua in considerare, nicio clipa, posibilitatea ca se inseala.
Prin urmare, nu numai ca P.A. e un numar matematic special – toate aparitiile sale autentice in matematica si Natura indica asta – dar are si o enorma importanta culturala, fiind unul din numerele fata de care oamenii au cele mai multe credinte gresite.
