Anul acesta a apărut la Editura Humanitas cartea „Fizica povestită”, care se doreşte o ambiţioasă trecere în revistă a principalelor concepte ale fizicii, într-o manieră accesibilă publicului. Lucrarea se adresează elevilor interesați de științele exacte din clasele a XI-a și a XII-a, studenţilor la profilele “beta”, precum şi pasionaţilor de ştiinţă, care posedă un bagaj minim de noţiuni de fizică. Autorul este Cristian Presura, un cunoscut al popularizării ştiinţei. Vă prezentăm mai jos un extract cu prima secţiune din carte; mai multe detalii despre carte se pot găsi la:
Anul acesta a apărut la Editura Humanitas cartea „Fizica povestită”, care se doreşte o ambiţioasă trecere în revistă a principalelor concepte ale fizicii, într-o manieră accesibilă publicului. Lucrarea se adresează elevilor interesați de științele exacte din clasele a XI-a și a XII-a, studenţilor la profilele “beta”, precum şi pasionaţilor de ştiinţă, care posedă un bagaj minim de noţiuni de fizică. Autorul este Cristian Presura, un cunoscut al popularizării ştiinţei. Vă prezentăm mai jos un extract cu prima secţiune din carte; mai multe detalii despre carte se pot găsi la:
http://stiinta.club/fizica-povestita
Obiectul fizicii este universul material în care trăim, iar scopul ei este în esenţă explicitarea comportamentului acestui univers. Pentru aceasta, fizica are nevoie de un limbaj şi de o metodă de analiză. În prima secţiune vom discuta puţin forma acestui limbaj (matematica) şi limitările sale. În secţiunile ce urmează vom exemplifica metoda de analiză cu ajutorul unor noţiuni de astronomie.
1 Limbajul naturii şi limitele sale
Einstein spunea odată că lucrul cel mai de neînţeles este că lumea poate fi înţeleasă. Ciudat, nu? Ne-am fi aşteptat ca lumea să fie o colecţie haotică de întâmplări singulare şi complet imprevizibile, un univers în care se poate întâmpla orice şi oricând. Dar universul îşi are legile lui, pe care oamenii de ştiinţă încearcă să le descopere.
Ploaia, de exemplu, cade mereu de sus în jos şi nu ne aşteptăm să ne punem umbrela sub picioare atunci când ieşim din casă. Există deci o lege a ploii, care ne spune că picăturile acesteia cad în jos. Fenomenul are loc mereu în acelaşi fel, în mod natural. Observaţia scoate în evidenţă o ordine în univers, ordine relevată de ştiinţă prin experimente repetabile.
Să observăm că ordinea universului o „citim” în limbajul matematicii. Dacă avem două monede de cinci lei, ştim că sunt în total zece lei. Dacă trenul pleacă din Bucureşti la o oră şi ştim cât de repede merge, putem prezice când ajunge la Râmnicu Vâlcea. Poziţia unei stele o măsurăm pe cer şi o scriem în caiet cu ajutorul unor numere. Putem prezice unde se va află steaua peste două ore, dacă luăm în calcul rotaţia boltei cereşti în jurul Pământului, adunând şi înmulţind numere.
Matematica stă la baza fizicii şi a modului de percepere a universului. Fără să numărăm nu putem aborda problema ordinii universului, iar fără să învăţăm să rezolvăm integrale nu vom rezolva ecuaţiile fizicii. Matematica este limbajulnaturii, aşa cum s-a afirmat adeseori.
Desigur, se prea poate ca această afirmaţie să fie falsă şi nişte extraterestri să găsească un alt limbaj al naturii. La urma urmei misticii au altă părere, spunând că universul este înţeles prin intuiţie, iar poeţii spun că universul ne „vorbeşte” prin frumuseţea naturii. În cartea de faţă noi ne vom limita la limbajul matematicii pentru a descoperi tainele universului material.
Matematicianul Bertrand Russell (1872-1970) a încercat să încapsuleze toată logica matematicii în cartea sa „Principia mathematica”, pentru a demonstra noncontradicţia şi completitudinea matematicii, fără să reuşească decât parţial. Pentru cei curioşi, „Principia mathematica” este o carte atipică. După o scurtă introducere, urmează mii de propoziţii logice care se deduc una din alta. Este ca şi cum Russell ar încerca să ne convingă că universul are o structură logică, ce se reconstruieşte folosind propoziţii logice deduse una din alta, cu ajutorul unor reguli definite dinainte.
Foarte încântaţi, mulţi oameni de ştiinţă au ridicat matematica în sfera abstractului, undeva dincolo de univers, necontaminată de timp şi spaţiu. Cu toate acestea, matematicianul Kurt Gödel (1906-1978) a demonstrat (culmea, matematic!) că şi matematica îşi are limitele ei. În esenţă, Gödel ne spune că matematica este un doar limbaj, care face parte din această lume şi care nu poate descrie complet însăşi lumea din care face parte. Cu alte cuvinte, nu ne aşteptăm să explicăm întreg universul, odată ce facem parte din el. Nu este nevoie să fim filozofi ca să ne dăm seama că, în acest caz, nu putem explica totul.
Matematica este o parte a acestei lumi, la fel cum eu sau dumneavoastră suntem parte a ei. Relaţia 1 + 1 = 2 este valabilă pentru toată lumea. Dacă pun un măr lângă altul, am două, oricine este de acord cu asta, atâta timp cât nu se întâmplă nimic fizic cu merele. Şi, fiindcă aşa stau lucrurile pentru toţi, cădem de acord şi construim limbajul matematicii. Cu toate acestea, pentru că matematica este o construcţie a lumii (în fond, o jonglerie cu mere), nu ne aşteptăm ca ea să descrie întreaga lume din care face parte.
Nu numai obiectele pe care le folosim fac parte din lume, dar chiar şi imaginaţia noastră este contaminată de lume, căci ea imită şi copiază comportamentul acestei lumi. Poetul german Johann Wolfgang Goethe spunea că noi nu inventăm nimic, ci doar redescoperim. De aceea nu ne aşteptăm ca matematica să poată explica complet însăşi lumea din care face parte şi care a creat-o, căci ar naşte contradicţii prin referinţe la ea însăşi.
Pentru a arăta de ce autoreferinţa este importantă, să considerăm enunţul „Propoziţia aceasta este falsă” şi să observăm că el nu este nici adevărat, nici fals. Dacă enunţul este adevărat, atunci propozitia este falsă, şi deci enunţul însuşi (la care face referire propoziţia) este fals, ajungându-se la o contradicţie. Dacă enunţul este fals, atunci propoziţia trebuie să fie adevărată, ceea ce implică automat ca şi enunţul (la care face referire propoziţia) trebuie să fie adevărat. Ajungem iarăşi la o contradicţie. Vedem astfel că enunţul precedent nu este nici adevărat, nici fals. Observăm însă că acest enunţ conţine o referinţă la el însuşi.
Într-un mod asemănător, Kurt Gödel a arătat la începutul secolului trecut că matematica conţine anumite propoziţii despre care nu se poate demonstra nici că sunt adevărate nici că sunt false, şi deci este incompletă. Metoda lui Gödel este pe cât de interesantă, pe atât de eficientă. Astfel, Gödel urmăreşte ideile lui Russell, care recunoaşte că matematica (şi în general orice fel de limbaj) este o colecţie de simboluri. Gödel însă are ideea genială de a considera că aceste simboluri sunt chiar numere!
Exemplul cel mai simplu este cel al jocului opera Gusti, un joc pe care copiii îl joacă pentru a-şi transmite mesaje „secrete”. În acest joc, o parte din litere sunt înlocuite cu cifre, prin identificarea „operagusti”=”1234567890”. De exemplu, cuvântul „toiag” se scrie ca „91056”. Desigur, în cazul jocului nu avem cifre suficiente să acoperim toate literele, aşa încât vom avea şi cuvinte precum „5c123409” sau „c5d”.
În cazul logicii matematice, Gödel a rescris toate propoziţiile logice cu numai şapte cifre, prin nişte artificii ingenioase, care au minimizat simbolurile folosite. Toate simbolurile de bază din propoziţiile logice, de exemplu „sau” şi cuvântul „egal”, erau descrise de una dintre cele şapte cifre. În final, fiecare propoziţie logică era exprimată printr-o succesiune de cifre, adică un număr. Adeverirea unei propoziţii este de asemenea reprezentată de un număr, iar negarea acelei propoziţii este un alt număr. Să remarcăm şi că o succesiune de propoziţii devine o succesiune de numere. A demonstra sau a nega o propoziţie se reduce la a găsi succesiunea de numere (conform unor reguli bine stabilite) care duce la unul din cele două numere care afirmă propoziţia sau o neagă.
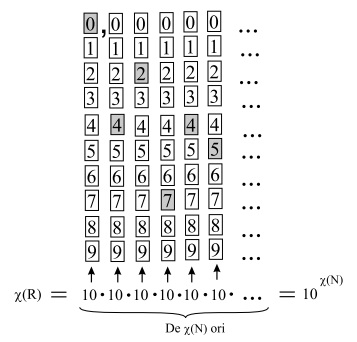 Figura 1: Câte numere reale avem? Pentru fiecare cifră a numărului real avem zece alegeri. În figură este exemplificat numărul real 0, 42745…. Numărul total χ(R) de numere reale este un produs al acestor posibilităţi χ(R) = 10⋅10⋅…⋅10⋅…. Dacă notăm cu χ(N) numărul infinit de elemente al mulţimii numerelor naturale, atunci avem χ(R) = 10^χ(N) . Interesant este că cele două numere χ(N) şi χ(R) sunt infinităţi diferite, pentru că nu poate fi găsită o relaţie bijectivă între mulţimile pe care le reprezintă.
Figura 1: Câte numere reale avem? Pentru fiecare cifră a numărului real avem zece alegeri. În figură este exemplificat numărul real 0, 42745…. Numărul total χ(R) de numere reale este un produs al acestor posibilităţi χ(R) = 10⋅10⋅…⋅10⋅…. Dacă notăm cu χ(N) numărul infinit de elemente al mulţimii numerelor naturale, atunci avem χ(R) = 10^χ(N) . Interesant este că cele două numere χ(N) şi χ(R) sunt infinităţi diferite, pentru că nu poate fi găsită o relaţie bijectivă între mulţimile pe care le reprezintă.
În principiu, ne-am aştepta ca orice propoziţie care poate fi formulată să fie nu numai falsă sau adevărată, dar şi demonstrabilă. În limbajul lui Gödel, aceasta înseamnă că pentru orice propoziţie logică trebuie să găsim o succesiune de numere care conduce la numărul ce reprezintă afirmaţia sau negaţia propoziţiei. Gödel însă a arătat că există propoziţii matematice pentru care nici unul dintre cele două numere (reprezentând afirmaţia sau negaţia propoziţiei) nu poate fi construit ca o succesiune de numere ale propoziţiilor intermediare. Cu alte cuvinte, matematica este incompletă, existând propoziţii despre care nu se poate demonstra nici că sunt false, nici că sunt adevărate.
Demonstraţia lui Gödel foloseşte faptul că metalimbajul (adică limbajul logicii) a devenit acum o succesiune de numere, succesiune căreia i se poate şi ei ataşa un alt număr. Pe de altă parte, acest metalimbaj (limbajul matematicii), scris cu numere, se referă tocmai la numere! Ne aflăm atunci într-o situaţie contradictorie, când vrem să descriem o lume (lumea numerelor, a matematicii) cu instrumente aparţinând aceleiaşi lumi (tot numere, simbolurile noastre, dar care descriu de această dată metalimbajul). Propoziţia construită de Gödel care nu poate fi demonstrată este de fapt enunţul menţionat de noi deja, „Propoziţia aceasta este falsă”, scris în metalimbajul numerelor şi care se referă tot la numere.
Teorema de incompletitudine a lui Gödel nu a rămas în aria filozofiei. Astfel, matematicienii chiar au găsit o propoziţie matematică care nu se poate demonstra nici că e falsă nici că e adevarată. Ea se referă la numărul de elemente pe care le au diferite mulţimi (finite sau infinite), număr ce poartă denumirea de cardinal în matematică.
Astfel, paradoxal, numărul infinit de elemente al mulţimii numerelor naturale (cardinalul numerelor naturale) este diferit de numărul infinit al elementelor mulţimii numerelor reale (cardinalul numerelor reale). Ciudat nu? Două numere infinite care sunt diferite. Acest lucru este posibil, pentru că nu există o relaţie bijectivă (unu la unu) între elementele celor două mulţimi.
Ne putem întreba dacă există mulţimi infinite al căror cardinal să se afle între cel al numerelor naturale şi cel al numerelor reale (care este evident mai mare). Asemănător teoremei lui Gödel, matematicienii au arătat că nu vom demonstra niciodată răspunsul la această întrebare, pentru că ea nu are o succesiune de propoziţii logice care să conducă la afirmarea sau negarea ei!
Este desigur fascinant să ştim cu siguranţă că nu putem demonstra vreodată răspunsul la o întrebare anume. În acest fel testăm în mod direct limitele cunoaşterii noastre umane prin intermediul matematicii.